Monday, August 6th.
 Andre-Marie TREMBLAY
Andre-Marie TREMBLAY
Mott transition, Hubbard model and superconductivity: an introduction.
Link to Blog

Ali YAZDANI
Visualizing the emergence of heavy fermions and their exotic properties
Link to Blog
Andre Marie began by discussing the great successes of the electronic theory of matter. Metals, band insulators and electron-phonon mediated metals. Metals and band-insulators - a triumph of Pauli's exclusion principle- even/odd no of electrons per unit cell gives an insulator/metal respectively. He discussed how the mean-field description of the pair operator gives rise to the phase of the superconductor -

Gradients of the phase of this order parameter describe the remarkable phenomenon of superconductivity.
But he then moved onto problems that can not be described using this framework. Mott insulators, quantum criticality, non-Fermi liquid behavior. Mott insulators - an idea due to Peierls and Mott - that when the Coulomb interaction exceeds the hopping, electrons localize. Quantum criticality - the strong quantum fluctuations that emerge at a zero temperature quantum phase transition. Non-Fermi liquid behavior - the departures from Fermi liquid behavior that appear to occur near a quantum critical point.
Andre introduced the phase diagram of the cuprates, which led to many questions. Such as
(1) can't you have a linear resistivity from phonons and band electrons? (An
(2) why is the region of the Antiferromagnet much larger with electron than hole doping? (Andre answered that hole doping is much more strongly coupled, and has more competing phases, such as charge order).
(3) is the critical temperature the same for hole and electron doping? (Andre-M. Yes it is if you chose (LaSr)CuO4 and (ReCe)CuO4 , as chosen in the figure).
(4) how does the phase diagram change with pressure? (Andre-M. Tc goes up with pressure holes, down with pressure, electrons).
(5) if you take anything that has antiferromagnetism, such as nickel or vanadium oxide, and you dope it to remove the afm - do you get a superconductor? (Andre-M: The case of VaO, it does not happen, but there are heavy fermion examples where it does occur - occurs -often, but not all the time?)
(6) what is the key parameter that drives superconductivity? (Andre-M: I will show you that in the one band Hubbard model, it is J that drives the sc).
AM contrasted the organics and the high temperature superconductors. In the former, pressure changes the bandwidth (ratio of t'/t), in the latter - it is doping controlled.
There are many properties he claimed, heavy fermions, high temperature supeconductivity, collosal magneto-resistance - that can not be explained with the Kohn Sham approach. There are many factors here - low dimension enhancing quantum and thermal fluctuations - large residual interactions. So how should one proceed in these cases? Answer - identify important physical principles to constrain non-perturbative approx. Benchmark against exact results. Check that weak and strong coupling match up at intermediate coupling. Last but not least - compare with experiment!
AM gave a selection of various methods:
Are cuprate superconductors truly doped Mott Insulators? , AM asked. AM constrasted the spectral weight transfer of regular and Mott insulators. Doping removes one state from the lower and the upper Mott band - not just a movement of chemical potential, a transfer of spectral weight from the upper to the lower band. He showed ARPES data that shows that the number of low energy states as 2x, not as 1+x as in Fermi liquids.
Next, AM discussed the Dynamical Mean Field Theory approach(DMFT) and the Cluster DMFT (C-DMFT) approach. He introduced the self-consistency eqns, and discussed the many waves of arriving at the same approach. In the Potthoff approach, one regards DMFT as a stationary point of a Luttinger-Ward functional F[G] under the restriction that the input Green function is local.
Q: Can one formalize a 1/D expansion beyond the infinite D limit as a way of correcting DMFT?
AM: Problems with causality have been encountered?
Q: A theory in infinite D is above the upper critical dimension, so how can one use DMFT?
AM: For critical phenomena, above the upper critical dimension, you would get mean-field phenomena, but below, you get non-mean field exponents. But here we're talking about fermions, so if you are in very large dimension, the main result is that the self-energy is only frequency dependent, not dependent on direction. If you just look at this fermion problem, as far as I can tell, there is no rigorous statement about what is the upper critical dimension. If you look at D=3, it turns out that the local approx seems to be good. If you look at two dimensions, we know that here the self-energy is strongly momentum dependent, and this is why you need clusters. But the other answer concerns higher order Greens functions - but whenever you compute them - you will always get mean field. Nobody yet knows how to include the corrections, the long-wavelength fluctuations, that become important below the upper critical dimension. This is one of the Frontiers of the field.
Q: What will happen if you're not exactly in 2D?
A: If you start from high temperature, the 3D aspects aren't important, but as you lower the T, they become more important.
Q: If you replace the k-integration by an integration over energy, this is fine for FL theory - and all information about the self-energy is lost. What happens here?
A: Lets discuss later.
Q: What is your opinion about the role of p-electrons in the cuprates?
AM: Indeed if we look at the pseudo-gap regime, you can see that the oxygen p-electrons are involved. Clearly, eventually it is important. Very close to half filling there is the idea of the Zhang Rice singlet, which though it contains O and Cu orbitals, it behaves as an effective "hole" in a one-band Hubbard model. Of course ultimately, we will have a three-band model.
AM then contrasted strong and weak-coupling in the Hubbard model at half filling, showing the spin-fluctuation scale versus U. At large U, for 4t^2/U < T < U, one has local moments. At low U, the transition is a Slater transition, but at high U, it is a Heisenberg phase transition. The upper transition at T~U is a Mott transition. In DMFT, one finds that the cross-over ends at a first order phase transition. The high-temperature limit is insensitive to lattice structure, and is very well described by DMFT. Clusters don't change much.
AM constrasted Fermi liquid based vs Mott insulator based approaches. In the DMFT/CDMT, one can treat long-range order in a mean-field way, but the detailed short-range dynamical and spatial correlations are well-described. The long-wavelength p-h and p-p fluctuations are lost.
Q: How do "C-DMFT" and "Extended DMFT" compare when you have RKKY interactions.
AM: I don't precisely know, but I can try to find the answer.
Q: Is the self-consistency like RPA?
AM: No, its better! But both don't satisfy the Mermin Wagner theory in 2D.
Summary: in the presence of correlation, we have lots of interesting new physics. This is at the heart of the problem in Organics, high temperature superconductors, heavy fermions and giant magneto-resistance. New methods to solve these problems are in very active development, and as time goes by, we start to understand the limitations of every method, and we're beginning to get convergence between strong and weak-coupling based approaches. In organic and high temperature superconductors, we have band-width and doping driven systems, but both are connected to the Mott transition.
Part II
In the afternoon, AM introduced the challenge of solving impurity problems, as a "solver" for C-DMFT. How does one do this? Conventional Monte Carlo has to deal with the fact that the weights for given quantum fluctuations are not positive definite. One has to factor out the sign of the
weight and include it into the observable
<A(x)> = Sum [A(x) Sign(p(x)) Abs[p(x)]/ Sum[Sign[p[x]] Abs[p[x]]]
This has the problem that when the sign changes a lot, the denominator becomes small and the errors become too large.
Instead, an alternative method is Monte-Carlo sampling of the diagramatic expansion of the partition function.
Z = Sum_config k Sum _other q nos Integral dtau1 ...dtauN w[k,tau]
The probabilities to add W[x->y] or remove a propagator W[y->x] is known, and one can use this to do a Monte-Carlo sampling of the perturbation theory. Using this method, one can now sample the diagram theory and it leads to a practical Monte Carlo method for evaluating correlation functions in imaginary time.
AM presented a summary of the formidable calculations that have been made using C-DMFT and the continuous time Monte Carlo. As a function of chemical potential, they see a sequence insulator -> metal 1 ->1st order transition -> metal 2. The metal 1 is interpreted as the pseudo-gap phase, and is seen to have a marked reduction in the density of states and the spin susceptibility. The first order transition forms a line that terminates at a finite T Ising transition.
AM mentioned that this approach does not include antiferromagnetism, which requires triplet correlations, which somehow are not included in this approach. There was a suggestion that the Mott phase captures the AFM region of the phase diagram.
AM also discussed superconductivity - here there is pairing at low doping, which I believe disappears at a rather low doping - AM suggested this is a consequence of using too small clusters. The size of the gap is very weakly doping dependent, in contrast with the physical superconductors. AM mentioned that it is still unclear what mechanism controls the dependence of Tc on doping in the cuprates.
Ali YAZDANI
Visualizing the emergence of heavy fermions and their exotic properties
 Ali then introduced the system CeCoIn5, which is a heavy fermion superconductor with a 2.5K transition temperature. This system appears to be almost quantum critical, as it displays a linear resistivity below about 40K. Ali showed the STM images of this system, showing that there are two important surfaces - the Ce-In surface ("A") and the Co surface ("B") . Surface C reconstructs and is not studied.
Ali then introduced the system CeCoIn5, which is a heavy fermion superconductor with a 2.5K transition temperature. This system appears to be almost quantum critical, as it displays a linear resistivity below about 40K. Ali showed the STM images of this system, showing that there are two important surfaces - the Ce-In surface ("A") and the Co surface ("B") . Surface C reconstructs and is not studied.
Remarkably, tunneling into the Ce layer is dominated by spd electrons, whereas tunneling into the Co surface is dominated by the co-tunneling, and shows a marked peak. The antiferromagnetic compound CeRhIn5 does not appear to contain delocalized heavy electrons, and no Kondo peak is seen at the Fermi surface.
Q: How can tunneling on the Co surface, which does not contain f-electrons be dominated by coupling to f-electrons.
AY: This is because of the cotunneling. The f-electrons are strongly hybridized with the Co layers, and cotunneling is dominated by the addition of electrons to the Co layers.
Ali then turned to the quasiparticle interference - the spatial structure of the tunneling. By following the Friedel oscillations on surface A, he showed that it was possible to image the development of hybridization with f-electrons. Surface B imaged the flat part of the band. In this way, it is possible to directly demonstrate the formation of a hybridized heavy fermion band.
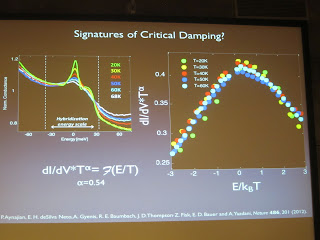
Ali finished with a discussion of the temperature dependence. Remarkably, the Kondo resonance imagaed on surface B (Co layer) narrows with temperature, and can be collapsed onto an E/T scaling plot. This is the STM counterpart of E/T scaling seen in the dynamical spin susceptibilty Au-doped quantum critical CeCu6-xAux. Ali speculated that this suggests some kind of local quantum criticality.
Whats next? The Yazdani group are cooling down to try and observe the development of superconductivity in CeCoIn5. This requires a new setup, combining a dilution fridge and new STM rig (with lots of isolation). We all look forward to seeing the results from this new machine (shown here).
 Andre-Marie TREMBLAY
Andre-Marie TREMBLAYMott transition, Hubbard model and superconductivity: an introduction.
Link to Blog

Ali YAZDANI
Visualizing the emergence of heavy fermions and their exotic properties
Link to Blog
Andre Marie began by discussing the great successes of the electronic theory of matter. Metals, band insulators and electron-phonon mediated metals. Metals and band-insulators - a triumph of Pauli's exclusion principle- even/odd no of electrons per unit cell gives an insulator/metal respectively. He discussed how the mean-field description of the pair operator gives rise to the phase of the superconductor -
Gradients of the phase of this order parameter describe the remarkable phenomenon of superconductivity.
But he then moved onto problems that can not be described using this framework. Mott insulators, quantum criticality, non-Fermi liquid behavior. Mott insulators - an idea due to Peierls and Mott - that when the Coulomb interaction exceeds the hopping, electrons localize. Quantum criticality - the strong quantum fluctuations that emerge at a zero temperature quantum phase transition. Non-Fermi liquid behavior - the departures from Fermi liquid behavior that appear to occur near a quantum critical point.
Andre introduced the phase diagram of the cuprates, which led to many questions. Such as
(1) can't you have a linear resistivity from phonons and band electrons? (An
(2) why is the region of the Antiferromagnet much larger with electron than hole doping? (Andre answered that hole doping is much more strongly coupled, and has more competing phases, such as charge order).
(3) is the critical temperature the same for hole and electron doping? (Andre-M. Yes it is if you chose (LaSr)CuO4 and (ReCe)CuO4 , as chosen in the figure).
(4) how does the phase diagram change with pressure? (Andre-M. Tc goes up with pressure holes, down with pressure, electrons).
(5) if you take anything that has antiferromagnetism, such as nickel or vanadium oxide, and you dope it to remove the afm - do you get a superconductor? (Andre-M: The case of VaO, it does not happen, but there are heavy fermion examples where it does occur - occurs -often, but not all the time?)
(6) what is the key parameter that drives superconductivity? (Andre-M: I will show you that in the one band Hubbard model, it is J that drives the sc).
AM contrasted the organics and the high temperature superconductors. In the former, pressure changes the bandwidth (ratio of t'/t), in the latter - it is doping controlled.
There are many properties he claimed, heavy fermions, high temperature supeconductivity, collosal magneto-resistance - that can not be explained with the Kohn Sham approach. There are many factors here - low dimension enhancing quantum and thermal fluctuations - large residual interactions. So how should one proceed in these cases? Answer - identify important physical principles to constrain non-perturbative approx. Benchmark against exact results. Check that weak and strong coupling match up at intermediate coupling. Last but not least - compare with experiment!
AM gave a selection of various methods:
- Weak coupling and renormalization. (FRG, Diagramatic methods, FLEX..)
- Renormalized Mean Field Theory
- Slave particles and Gauge Theories
- Variational Approaches
- Cluster and Dynamical Mean field approaches.
Are cuprate superconductors truly doped Mott Insulators? , AM asked. AM constrasted the spectral weight transfer of regular and Mott insulators. Doping removes one state from the lower and the upper Mott band - not just a movement of chemical potential, a transfer of spectral weight from the upper to the lower band. He showed ARPES data that shows that the number of low energy states as 2x, not as 1+x as in Fermi liquids.
Next, AM discussed the Dynamical Mean Field Theory approach(DMFT) and the Cluster DMFT (C-DMFT) approach. He introduced the self-consistency eqns, and discussed the many waves of arriving at the same approach. In the Potthoff approach, one regards DMFT as a stationary point of a Luttinger-Ward functional F[G] under the restriction that the input Green function is local.
Q: Can one formalize a 1/D expansion beyond the infinite D limit as a way of correcting DMFT?
AM: Problems with causality have been encountered?
Q: A theory in infinite D is above the upper critical dimension, so how can one use DMFT?
AM: For critical phenomena, above the upper critical dimension, you would get mean-field phenomena, but below, you get non-mean field exponents. But here we're talking about fermions, so if you are in very large dimension, the main result is that the self-energy is only frequency dependent, not dependent on direction. If you just look at this fermion problem, as far as I can tell, there is no rigorous statement about what is the upper critical dimension. If you look at D=3, it turns out that the local approx seems to be good. If you look at two dimensions, we know that here the self-energy is strongly momentum dependent, and this is why you need clusters. But the other answer concerns higher order Greens functions - but whenever you compute them - you will always get mean field. Nobody yet knows how to include the corrections, the long-wavelength fluctuations, that become important below the upper critical dimension. This is one of the Frontiers of the field.
Q: What will happen if you're not exactly in 2D?
A: If you start from high temperature, the 3D aspects aren't important, but as you lower the T, they become more important.
Q: If you replace the k-integration by an integration over energy, this is fine for FL theory - and all information about the self-energy is lost. What happens here?
A: Lets discuss later.
Q: What is your opinion about the role of p-electrons in the cuprates?
AM: Indeed if we look at the pseudo-gap regime, you can see that the oxygen p-electrons are involved. Clearly, eventually it is important. Very close to half filling there is the idea of the Zhang Rice singlet, which though it contains O and Cu orbitals, it behaves as an effective "hole" in a one-band Hubbard model. Of course ultimately, we will have a three-band model.
AM then contrasted strong and weak-coupling in the Hubbard model at half filling, showing the spin-fluctuation scale versus U. At large U, for 4t^2/U < T < U, one has local moments. At low U, the transition is a Slater transition, but at high U, it is a Heisenberg phase transition. The upper transition at T~U is a Mott transition. In DMFT, one finds that the cross-over ends at a first order phase transition. The high-temperature limit is insensitive to lattice structure, and is very well described by DMFT. Clusters don't change much.
AM constrasted Fermi liquid based vs Mott insulator based approaches. In the DMFT/CDMT, one can treat long-range order in a mean-field way, but the detailed short-range dynamical and spatial correlations are well-described. The long-wavelength p-h and p-p fluctuations are lost.
Q: How do "C-DMFT" and "Extended DMFT" compare when you have RKKY interactions.
AM: I don't precisely know, but I can try to find the answer.
Q: Is the self-consistency like RPA?
AM: No, its better! But both don't satisfy the Mermin Wagner theory in 2D.
Summary: in the presence of correlation, we have lots of interesting new physics. This is at the heart of the problem in Organics, high temperature superconductors, heavy fermions and giant magneto-resistance. New methods to solve these problems are in very active development, and as time goes by, we start to understand the limitations of every method, and we're beginning to get convergence between strong and weak-coupling based approaches. In organic and high temperature superconductors, we have band-width and doping driven systems, but both are connected to the Mott transition.
Part II
In the afternoon, AM introduced the challenge of solving impurity problems, as a "solver" for C-DMFT. How does one do this? Conventional Monte Carlo has to deal with the fact that the weights for given quantum fluctuations are not positive definite. One has to factor out the sign of the
weight and include it into the observable
<A(x)> = Sum [A(x) Sign(p(x)) Abs[p(x)]/ Sum[Sign[p[x]] Abs[p[x]]]
This has the problem that when the sign changes a lot, the denominator becomes small and the errors become too large.
Instead, an alternative method is Monte-Carlo sampling of the diagramatic expansion of the partition function.
Z = Sum_config k Sum _other q nos Integral dtau1 ...dtauN w[k,tau]
The probabilities to add W[x->y] or remove a propagator W[y->x] is known, and one can use this to do a Monte-Carlo sampling of the perturbation theory. Using this method, one can now sample the diagram theory and it leads to a practical Monte Carlo method for evaluating correlation functions in imaginary time.
AM presented a summary of the formidable calculations that have been made using C-DMFT and the continuous time Monte Carlo. As a function of chemical potential, they see a sequence insulator -> metal 1 ->1st order transition -> metal 2. The metal 1 is interpreted as the pseudo-gap phase, and is seen to have a marked reduction in the density of states and the spin susceptibility. The first order transition forms a line that terminates at a finite T Ising transition.
AM mentioned that this approach does not include antiferromagnetism, which requires triplet correlations, which somehow are not included in this approach. There was a suggestion that the Mott phase captures the AFM region of the phase diagram.
AM also discussed superconductivity - here there is pairing at low doping, which I believe disappears at a rather low doping - AM suggested this is a consequence of using too small clusters. The size of the gap is very weakly doping dependent, in contrast with the physical superconductors. AM mentioned that it is still unclear what mechanism controls the dependence of Tc on doping in the cuprates.
Ali YAZDANI
Visualizing the emergence of heavy fermions and their exotic properties
Ali Yazdani introduced the basic ideas of tunneling. He stressed the importance of correlating observations with bulk measurements, to convince oneself that one is measuring bulk properties. Very important that the tip density of states and the tunneling matrix element is very weakly energy dependent. He showed how one can use the method for imaging and spectroscopy as a function of position: 2D maps. This sort of measurement takes a few seconds for a single spectrum, hundred energy points, 256 x 256 pixels over 1000 Angstroms takes four or five days, and one needs excellent vibration in a bunker. Low frequency noise is a particular problem.
Q: How big is the tip at the end? How many atoms?
AY: You pick a simple tip, such as Iridium, which makes nice tips. You can heat the tip, sputter it to clean it. You can poke it into to copper to make it atomically sharp. The identity of the tip atom is actually unknown.
Ali showed the Friedel oscillation standing waves - in momentum space you can think of the electrons living on the Fermi surface - when they hit a defect, they backscatter around the simple Fermi surface. You can get info about the FS if you study how they scatter off defects. By Fourier transfering the real-space picture, you can for example, image the 111 surface state of Cu. More complex examples are the topological surface states of a topological insulator. Regions of high density of states dominate the interference pattern.
Q: Are you touching the surface of the sample?
AY: There is a gap of about 6A, you can stay fairly far away and get 100's of pA of current, easily measured?
Q: Do you need to prepare the surface of the sample?
AY: You have to prepare a clean surface in a vacuum. All these expts - surface mostly by breaking the crystal in a vacuum.
Q: How do you distinguish structural from electronic features?
AY: On samples that are cleaved flat, once you see a step, you can correlate that with structural features. But if there is structural reconstruction - it normally affects the spectrum over a large energy window, whereas electronic features are usually strongly energy dependent.
Q: How do you distinguish electrons, the Fermi surface and nearby states?
AY: We have excellent energy resolution. I can show you tunneling into semiconductors and s-wave scs, and they behave in ways we understand. You can also see the effects of defects, and these also behave in ways we can understand?
Now Ali turned to the cuprates. He went over the main questions - the things that are poorly understood. There is a region of fluctuating superconductivity and at high temperatures the pseudogap phase, with some kind of competing order. Similar features are seen in iron-based and heavy fermion superconductors. "Our group has developed the electronics to be able to take the measurements up to 100K, while maintaining atomic registry. "
At low doping there is evidence for exotic ordered phases, such as stripes at 12.5%. He said we know that these are d-wave superconductors, from Josephson corner-junction measurements that determine the phase change across the pair wavefunction. What is really difficult to understand is the evolution of the Fermi surface from high doping to low doping. The Large Fermi surface seems to get partially lost in the antinodes at low doping, where a gap opens up in the pseudo-gap state, leaving nodal states ungapped. The key question is the pairing mechanism and how we connect this with the pseudogap physics? What is the interaction of the pseudogap with the sc? Is it a friend or Fo?
Most of the STM work on cuprates, is on the Bismuth Strontium Calcium Copper Oxide (Bi2Sr2CaCu2O8+\delta), which cleaves very well to give images like the following. You can see the structural distortion which is strongest in the Bi-O layer.Different gaps develop at different temperatures corresponding to local gap and scattering rates.
Ali also showed the suppession of SC in underdoped cuprates. Corroborated with the most reecent ARPES. The nodal gap separates from simple d-wave in the under-doped systems. The separation point in both ARPES and STM defines a "Fermi surface arc" which grows with doping, until it covers the entire Fermi surface. Along the arc regions, one obtains a d-wave gap.What we could talk about in discussion, is the spatial structure - there's a lot of spatial structure probably connected with competing order - such as stripes. This afternoon we'll switch to another topic.
Ali showed the Friedel oscillation standing waves - in momentum space you can think of the electrons living on the Fermi surface - when they hit a defect, they backscatter around the simple Fermi surface. You can get info about the FS if you study how they scatter off defects. By Fourier transfering the real-space picture, you can for example, image the 111 surface state of Cu. More complex examples are the topological surface states of a topological insulator. Regions of high density of states dominate the interference pattern.
Q: Are you touching the surface of the sample?
AY: There is a gap of about 6A, you can stay fairly far away and get 100's of pA of current, easily measured?
Q: Do you need to prepare the surface of the sample?
AY: You have to prepare a clean surface in a vacuum. All these expts - surface mostly by breaking the crystal in a vacuum.
Q: How do you distinguish structural from electronic features?
AY: On samples that are cleaved flat, once you see a step, you can correlate that with structural features. But if there is structural reconstruction - it normally affects the spectrum over a large energy window, whereas electronic features are usually strongly energy dependent.
Q: How do you distinguish electrons, the Fermi surface and nearby states?
AY: We have excellent energy resolution. I can show you tunneling into semiconductors and s-wave scs, and they behave in ways we understand. You can also see the effects of defects, and these also behave in ways we can understand?
Now Ali turned to the cuprates. He went over the main questions - the things that are poorly understood. There is a region of fluctuating superconductivity and at high temperatures the pseudogap phase, with some kind of competing order. Similar features are seen in iron-based and heavy fermion superconductors. "Our group has developed the electronics to be able to take the measurements up to 100K, while maintaining atomic registry. "
At low doping there is evidence for exotic ordered phases, such as stripes at 12.5%. He said we know that these are d-wave superconductors, from Josephson corner-junction measurements that determine the phase change across the pair wavefunction. What is really difficult to understand is the evolution of the Fermi surface from high doping to low doping. The Large Fermi surface seems to get partially lost in the antinodes at low doping, where a gap opens up in the pseudo-gap state, leaving nodal states ungapped. The key question is the pairing mechanism and how we connect this with the pseudogap physics? What is the interaction of the pseudogap with the sc? Is it a friend or Fo?
Most of the STM work on cuprates, is on the Bismuth Strontium Calcium Copper Oxide (Bi2Sr2CaCu2O8+\delta), which cleaves very well to give images like the following. You can see the structural distortion which is strongest in the Bi-O layer.Different gaps develop at different temperatures corresponding to local gap and scattering rates.
Ali also showed the suppession of SC in underdoped cuprates. Corroborated with the most reecent ARPES. The nodal gap separates from simple d-wave in the under-doped systems. The separation point in both ARPES and STM defines a "Fermi surface arc" which grows with doping, until it covers the entire Fermi surface. Along the arc regions, one obtains a d-wave gap.What we could talk about in discussion, is the spatial structure - there's a lot of spatial structure probably connected with competing order - such as stripes. This afternoon we'll switch to another topic.
Part II: Heavy Fermions
In the afternoon, Ali turned to the study of Heavy Fermions, and in particular, the heavy fermion system CeCoIn5. AY discussed the idea of the Kondo effect, in which a spin is screened by forming an entangled singlet with the surrounding conduction sea.
In the afternoon, Ali turned to the study of Heavy Fermions, and in particular, the heavy fermion system CeCoIn5. AY discussed the idea of the Kondo effect, in which a spin is screened by forming an entangled singlet with the surrounding conduction sea.
He then discussed how this idea can be generalized to the
idea of a "Kondo Lattice", in which the local moments delocalize their
spin into the conduction sea to form a large Fermi surface of heavy
fermions. He pointed out that with the exception of the hidden order system URu2Si2, this process has never been
microscopically imaged using STM methods.
 One of the important concepts for his talk, is the idea that tunneling into heavy fermions goes via two paths - a direct tunneling into the spd electrons, and a "cotunneling" into the f-electrons - a process that really involves the correlated addition of an electron and a spin-flip of a localized f-electron, which once coherent, can be thought of as tunneling into the f-state. These two processes interfere. When both processes are present, it leads to an interference or "Fano shaped" line. If the coupling to the spd electrons dominates, this produces a "dent" in the density of states. But if the cotunneling dominates, the process can image the Kondo resonance near the Fermi surface. (Strong coupling to f-electrons).
One of the important concepts for his talk, is the idea that tunneling into heavy fermions goes via two paths - a direct tunneling into the spd electrons, and a "cotunneling" into the f-electrons - a process that really involves the correlated addition of an electron and a spin-flip of a localized f-electron, which once coherent, can be thought of as tunneling into the f-state. These two processes interfere. When both processes are present, it leads to an interference or "Fano shaped" line. If the coupling to the spd electrons dominates, this produces a "dent" in the density of states. But if the cotunneling dominates, the process can image the Kondo resonance near the Fermi surface. (Strong coupling to f-electrons).
 One of the important concepts for his talk, is the idea that tunneling into heavy fermions goes via two paths - a direct tunneling into the spd electrons, and a "cotunneling" into the f-electrons - a process that really involves the correlated addition of an electron and a spin-flip of a localized f-electron, which once coherent, can be thought of as tunneling into the f-state. These two processes interfere. When both processes are present, it leads to an interference or "Fano shaped" line. If the coupling to the spd electrons dominates, this produces a "dent" in the density of states. But if the cotunneling dominates, the process can image the Kondo resonance near the Fermi surface. (Strong coupling to f-electrons).
One of the important concepts for his talk, is the idea that tunneling into heavy fermions goes via two paths - a direct tunneling into the spd electrons, and a "cotunneling" into the f-electrons - a process that really involves the correlated addition of an electron and a spin-flip of a localized f-electron, which once coherent, can be thought of as tunneling into the f-state. These two processes interfere. When both processes are present, it leads to an interference or "Fano shaped" line. If the coupling to the spd electrons dominates, this produces a "dent" in the density of states. But if the cotunneling dominates, the process can image the Kondo resonance near the Fermi surface. (Strong coupling to f-electrons).  Ali then introduced the system CeCoIn5, which is a heavy fermion superconductor with a 2.5K transition temperature. This system appears to be almost quantum critical, as it displays a linear resistivity below about 40K. Ali showed the STM images of this system, showing that there are two important surfaces - the Ce-In surface ("A") and the Co surface ("B") . Surface C reconstructs and is not studied.
Ali then introduced the system CeCoIn5, which is a heavy fermion superconductor with a 2.5K transition temperature. This system appears to be almost quantum critical, as it displays a linear resistivity below about 40K. Ali showed the STM images of this system, showing that there are two important surfaces - the Ce-In surface ("A") and the Co surface ("B") . Surface C reconstructs and is not studied. Remarkably, tunneling into the Ce layer is dominated by spd electrons, whereas tunneling into the Co surface is dominated by the co-tunneling, and shows a marked peak. The antiferromagnetic compound CeRhIn5 does not appear to contain delocalized heavy electrons, and no Kondo peak is seen at the Fermi surface.
Q: How can tunneling on the Co surface, which does not contain f-electrons be dominated by coupling to f-electrons.
AY: This is because of the cotunneling. The f-electrons are strongly hybridized with the Co layers, and cotunneling is dominated by the addition of electrons to the Co layers.
Ali then turned to the quasiparticle interference - the spatial structure of the tunneling. By following the Friedel oscillations on surface A, he showed that it was possible to image the development of hybridization with f-electrons. Surface B imaged the flat part of the band. In this way, it is possible to directly demonstrate the formation of a hybridized heavy fermion band.
Ali finished with a discussion of the temperature dependence. Remarkably, the Kondo resonance imagaed on surface B (Co layer) narrows with temperature, and can be collapsed onto an E/T scaling plot. This is the STM counterpart of E/T scaling seen in the dynamical spin susceptibilty Au-doped quantum critical CeCu6-xAux. Ali speculated that this suggests some kind of local quantum criticality.
Whats next? The Yazdani group are cooling down to try and observe the development of superconductivity in CeCoIn5. This requires a new setup, combining a dilution fridge and new STM rig (with lots of isolation). We all look forward to seeing the results from this new machine (shown here).